衡泰xAsset多因子系统,自2022年启动研发,经过三年多模型与功能的持续迭代,现已构建完成国内独家的A+H股及A股多因子模型,实现模型本土化、自动化、定制化的同时,计算精度比肩国际一流供应商,为机构投资业务和风控人员,提供全方位专业的投资能力与投资组合业绩评价模型和功能,赋能资管行业风险管理及价值创造。
作为全球范围内大型资管公司等机构的标配,多因子模型(MFM)及其系统渗透到投资决策各个环节,提供系统化、可量化的全面投资框架,也对数据处理、模型构建等方面提出了极高的技术专业性要求。
本文重点介绍了衡泰H股多因子风险模型xHK1的构建方法,并在实证部分从多个维度评估了衡泰xHK1模型在港股市场的表现,包括:模型的整体拟合度、因子收益率的波动性,以及因子解释力的显著性和稳健性。实证结果表明,衡泰xHK1模型在港股市场表现良好,全市场模型的平均拟合度达到20%。
作者:衡泰多因子团队
(吴卫东博士等)
01
多因子模型简介
1.1 投资组合风险与收益
投资管理是平衡风险与收益的决策过程,无论是资产配置、主动组合管理、被动组合管理,亦或是定性和定量投资,投资者在追求高额收益的同时需要合理控制风险。超额收益本质是对承担额外风险的补偿,我们在评价超额收益的同时也要分析组合承担的风险。
风险衡量投资收益率的不确定性,可以定义为资产收益率分散或波动程度。业界最标准的风险定义是采用收益率的标准差。马科维茨首次采用统计方法对投资风险进行量化,并证明组合的风险不大于其成分证券的风险总和。
但是马科维兹的均值方差风险模型存在一定局限性,假设组合有N 只股票构成,股票收益率协方差矩阵参数个数则为N× (N− 1)/2,随着N 的增长,计算复杂度将以N2 级别增长。
随着风险模型的不断发展,投资组合风险分析体系日趋完善,多因子风险模型应运而生并发展成为投资组合分析的有力工具。
多因子模型本质是降维,将对于高维股票的收益/风险预测转换为对于低维因子的收益/风险预测,不仅可以大大减少计算量,还能够有效提高风险预测的准确度。风险归因是多因子模型所特有的分析方法,传统的Brinson归因只能做绩效归因。
1.2 多因子模型
根据Barra 最新版的USE4风险模型,我们可以把任何股票的收益率归因到几个不同的风险因子上,包括市场(国家)因子、风格因子和行业因子,具体公式如下:
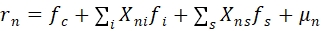 (1.1)
(1.1)
其中,fc 是市场(国家)因子的收益,fi 是行业因子i的收益,fs 是风格因子s 的收益,Xni , Xns 是各行业和风格因子的暴露,μn是个股的特质收益,USE4中采用加权最小二乘回归法WLS估计因子收益,其假设个股特质收益的方差为市值平方根的倒数(源于股票的特质风险随公司市值增加而减小的经验观察)。
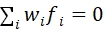 (1.2)
(1.2)
其中,wi 表示行业i 中所有股票流通市值占全市场股票流通市值的比例,约束条件的选择不会影响模型拟合,也不会影响模型的解释力,但其会对因子解释产生直接的影响。这个约束条件其实有比较直观的解释:考虑一个流通市值加权的投资组合P,持仓股票的权重记为![]() ,投资组合的收益Rp 可以写成:
,投资组合的收益Rp 可以写成:
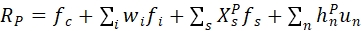

其中![]() ,是风格因子s的因子暴露,然而,由(1.2)可知,行业因子收益和为0,方程(1.3)的第一个求和项(
,是风格因子s的因子暴露,然而,由(1.2)可知,行业因子收益和为0,方程(1.3)的第一个求和项(![]() )为0,类似的风格因子市值加权也被标准化到均值为0,即(1.3)的第二个求和项(
)为0,类似的风格因子市值加权也被标准化到均值为0,即(1.3)的第二个求和项(![]() )也为0,最后一个求和项
)也为0,最后一个求和项![]() 对应于一个分散化投资组合的特质收益率,因此其和也接近0, 因此,(1.3)可以近似等价为: RP≈ fc。换句话说,市场因子(国家因子,截距项)代表了市值加权的全市场组合收益。
对应于一个分散化投资组合的特质收益率,因此其和也接近0, 因此,(1.3)可以近似等价为: RP≈ fc。换句话说,市场因子(国家因子,截距项)代表了市值加权的全市场组合收益。
然后我们根据(1.1)和(1.2)使用加权最小二乘法WLS进行模型估算,因子收益率的估计值可由(1.4)给出:
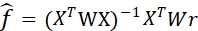 (1.4)
(1.4)
其中,W 为回归权重(对角线矩阵),![]() ,其中CAPn为第n 只股票的流通市值,X 是风险因子的因子暴露,r 是股票的个股收益率。
,其中CAPn为第n 只股票的流通市值,X 是风险因子的因子暴露,r 是股票的个股收益率。
个股权重为w (w 为N *1 的矩阵)的投资组合的波动率如下:
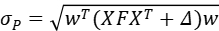
其中,X 表示N 只个股在K个风险因子上的因子载荷矩阵(N * K),F 表示因子收益率的协方差矩阵(K * K),
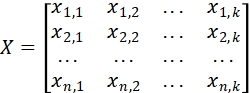
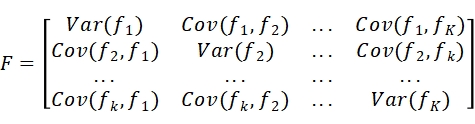
delta表示因子的特异收益率方差矩阵(N * N 的对角阵)。
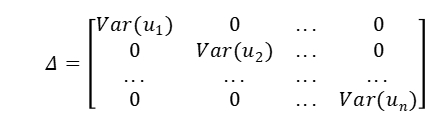
02
衡泰H股多因子模型xHK1
我们参考Barra CXE1模型的18个风格因子,将全球行业分类替换为更适合中国资本市场的申万行业分类,构建衡泰H股多因子风险模型xHK1。使用横截面回归计算因子收益率和特异性收益率,进而估计因子收益协方差矩阵和特异性收益方差矩阵。
在计算因子暴露的过程中,我们的研究团队对每一个因子,每一个descriptor的计算细节保持了极致的细致,总是使用双重或多重复核,确保因子暴露计算的准确性。因子暴露的计算是多因子风险模型的基石,是后续绩效风险归因和组合优化的重要基础。
2.1 因子分类及数据处理方法
风格因子分类及释义如下表所示:
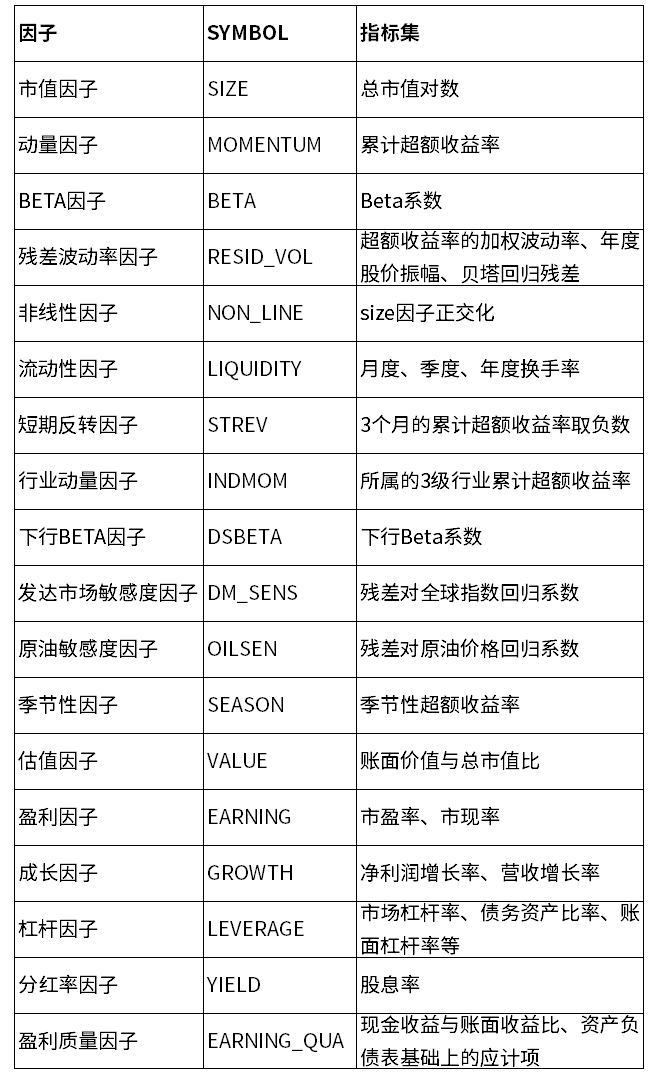
行业因子采用本土化的申万行业分类:
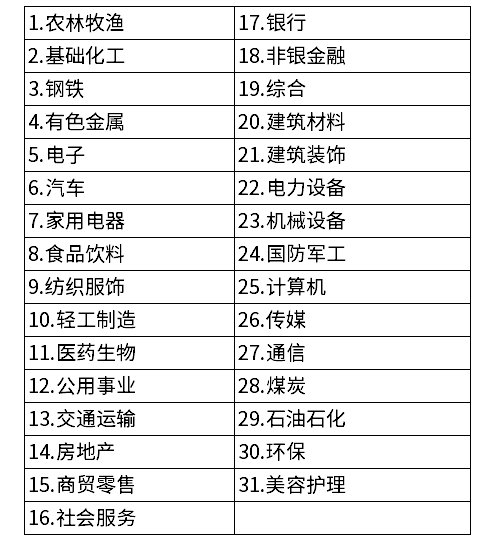
部分风格因子的构成方式并非单一指标,而是由多个明细因子(descriptor)加权组合构成,为保证数据的纲量一致,我们需要对因子进行标准化处理。为避免极端值(outlier)对标准化的影响,采用“中位数去极值法(MAD)”计算上下阈值,同时将超过阈值的极端值用阈值替代(拉回到阈值)。
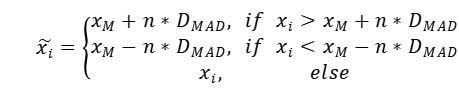
![]() : 序列xi 的中位数
: 序列xi 的中位数
![]() :序列|xi−xM|的中位数
:序列|xi−xM|的中位数
![]() :xi 去极值修正后的值
:xi 去极值修正后的值
对于去极值后的数据再进行缺失值替换和标准化,此处均值采用市值加权均值,标准差采用等权标准差。整个数据处理全流程包括去极值,缺失值替换,标准化,和正交化四个步骤。
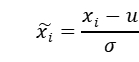
![]() :序列xi 的均值
:序列xi 的均值
![]() :序列xi 的标准差
:序列xi 的标准差
![]() :序列xi 的标准化之后的值
:序列xi 的标准化之后的值
2.2 多因子模型回归
传统多因子模型回归过程中同时加入风格因子、国家因子、行业因子,为消除国家因子和行业因子间共线性的影响,我们采用无截距项回归,计算出行业因子绝对收益率,再采用行业市值加权计算国家因子收益率,最后的行业因子收益率需减去国家因子收益率,得到行业超额因子收益率。
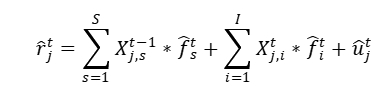
![]() :股票 j 在 t 期的收益率
:股票 j 在 t 期的收益率
![]() :股票在t-1期的风格因子s上的暴露度
:股票在t-1期的风格因子s上的暴露度
![]() :t 期风格因子s 的收益率
:t 期风格因子s 的收益率
![]() :股票j 在t 期行业因子i 的暴露度
:股票j 在t 期行业因子i 的暴露度
![]() :t 期行业因子i 的收益率
:t 期行业因子i 的收益率
![]() :股票 j 在t 期的残差收益率
:股票 j 在t 期的残差收益率
上式给出的行业因子收益率是假设国家因子为0(无截距项),且不约束行业因子收益率。所以,必须按照如下进一步计算国家因子fc 和fi(Wi 为个股流通市值占全市场股票流通市值的比例):
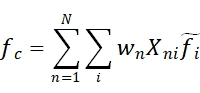
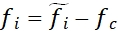
03
衡泰xHK1模型市场实证
3.1 风险因子评估体系
- α因子是对股票的预期收益率有稳定预测能力的因子,其因子收益率的均值显著不为0;
- 非α因子是对未来收益没有预测能力,其因子收益率的均值为0,需要在组合投资中进行控制暴露的因子。
通常,一个α因子被市场里越来越多的投资者所认知和运用之后,失去能带来稳定收益率的能力,就变成非α因子。比如中国市场的市值因子近年来开始显露其风险属性,而这此之前曾被很多投资者当做α因子。由于中国资本市场并不成熟,有些成熟市场的非α因子在中国市场则属于α因子。
我们可以从下面几个方面来评估风险因子:
1) 因子收益率的波动较大。因子收益率波动大,说明该因子会增加组合的波动风险,应该被归为风险因子,而因子收益率波动小的因子或者某些波动大但 Sharpe 值较高的因子会被归类为 Alpha 因子。
2) 因子解释力的显著性和稳健性。多因子模型要求风险因子应满足在每期横截面上的因子收益率较显著。具体方法是用每期的个股收益率对多个因子暴露度做回归,得到每个因子的T值再求出各期绝对值的均值,检验因子回归系数是否显著(T 值绝对值的平均值较大,一般设为 2),再看显著的月份占比有多少(一般计算|T值|大于2的占比)。
3)因子对港股收益率的整体解释度:调整后拟合优度(Adj Total R-Square)。这里需要特别强调的是Barra对调整R-Square 是用“非中心化”拟合优度(Total R-Square)来定义的,而常规计量学中的定义为“中心化”拟合优度(Relative R-Square)。
计量常用定义:Relative R-Square = 中心化拟合优度 = 1 - 残差平方和 / 离差平方和
Barra 模型定义:Total R-Square = 非中心化拟合优度 = 1 - 残差平方和 / y的平方和
从经验上,非中心化拟合优度要比中心化拟合优度数值大一些。Adjust R2和R2的关系如下:
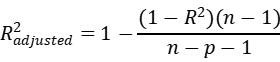
其中n是股票数量,p是回归自变量的数量。因为股票数量远大于自变量数量,Adj-Total-R2和Total-R2基本一样;同样地,Adj-Relative-R2和Relative-R2基本一样。
3.2 风险因子的回归显著性检验
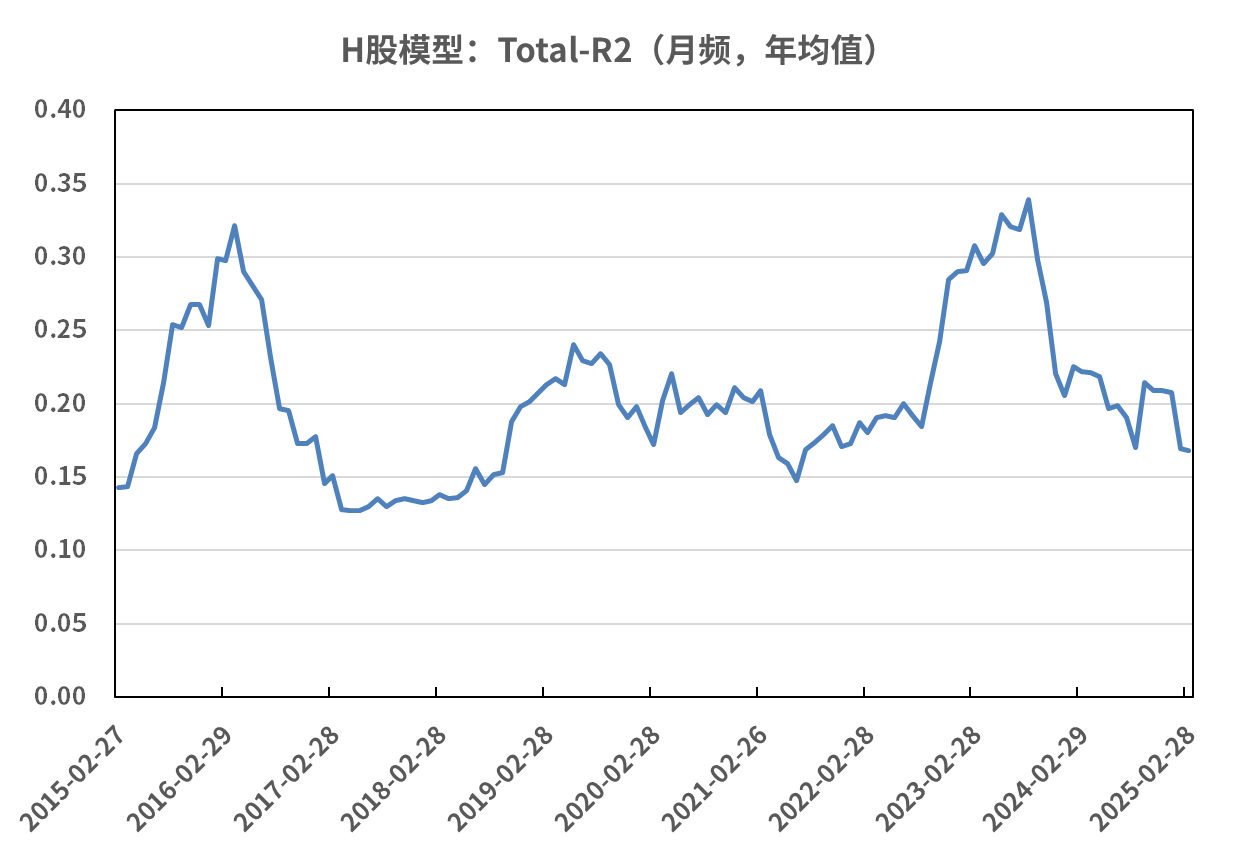
为检测模型的有效性,我们计算全市场模型的月频回归的滚动12月拟合度(Total-R-Square),样本覆盖时间区间为2015年2月至2025年2月。
总体看来, 衡泰多因子模型的全市场整体平均拟合度Total-R2达到20%。港股模型的拟合度0.20低于A股模型的平均拟合度0.36,这可能是因为H股的流动性相对更差,股价更容易被短期情绪推动而偏离合理价格或者被人为操纵。
图1. 月频拟合度12个月滚动均值
数据来源:衡泰一数通、财汇、衡泰研究部
对于全市场模型的因子显著性的稳健度检验,我们采用因子回归显著(即回归|T|大于2)的周期数量除以总回归周期数量得到因子回归显著性占比(即回归|T|大于2的占比)。
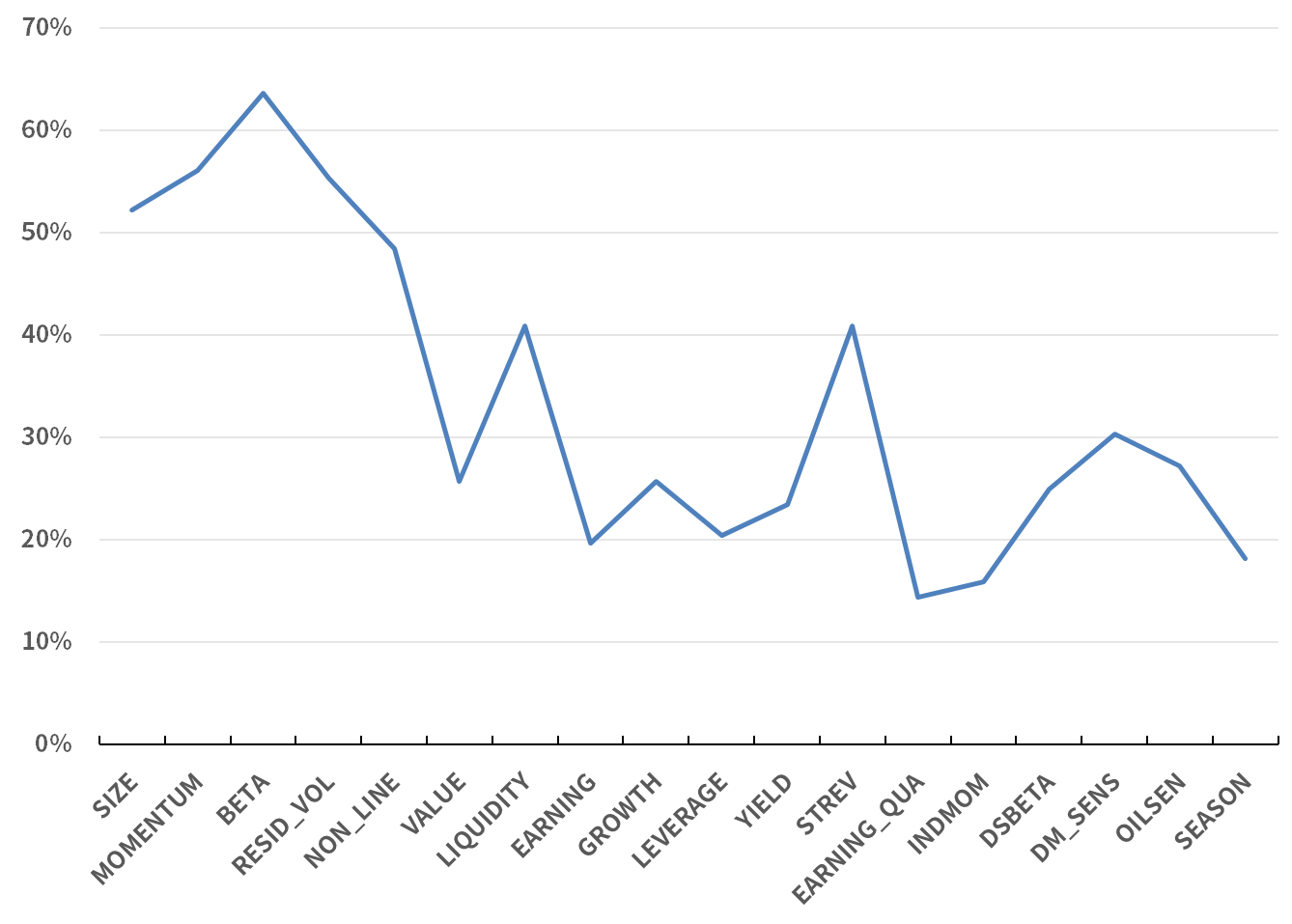
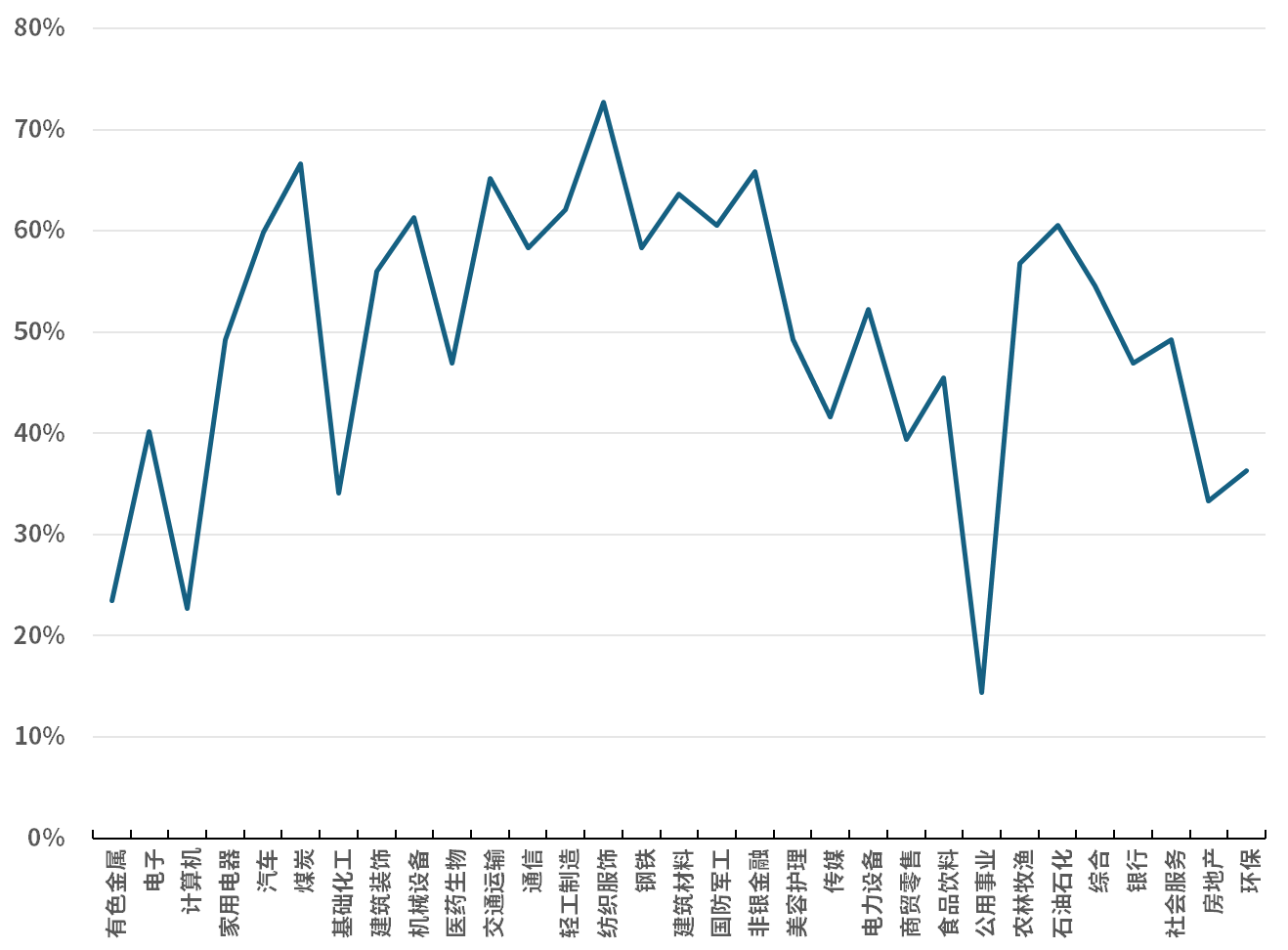
10个风格因子的显著性占比的均值为35%(图2),18个行业因子的显著性占比的均值为50%(图3),说明行业因子整体对股票收益率的解释更为稳定,这也说明行业因子是风险模型中重要的因子。
图2. 风格因子回归显著性占比%
数据来源:衡泰一数通、财汇、衡泰研究部
图3. 行业因子回归显著性占比%
数据来源:衡泰一数通、财汇、衡泰研究部
3.3 风险因子收益率的年化波动率
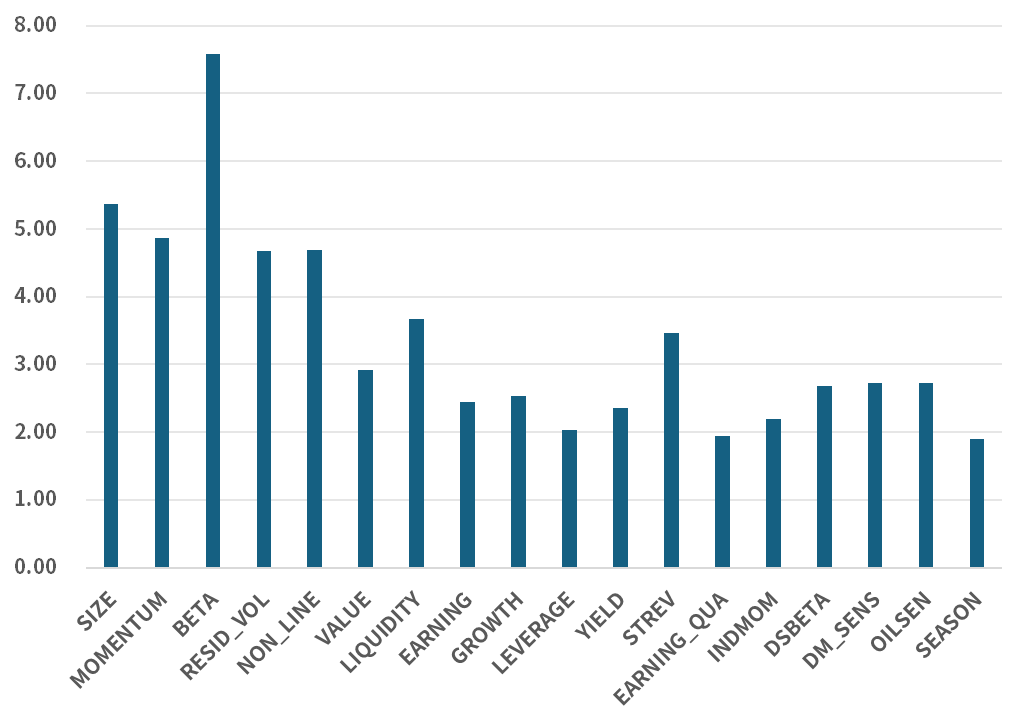
我们对港股市场的18个风格因子和申万31个一级行业分类因子进行分析,计算月频因子收益率的年化波动率(图4和图5)。风格因子年化波动率的均值为3.37%,行业因子年化波动率的均值为12.05%。
图4. 风格因子年化波动率%
数据来源:衡泰一数通、财汇、衡泰研究部
图5. 行业因子年化波动率%
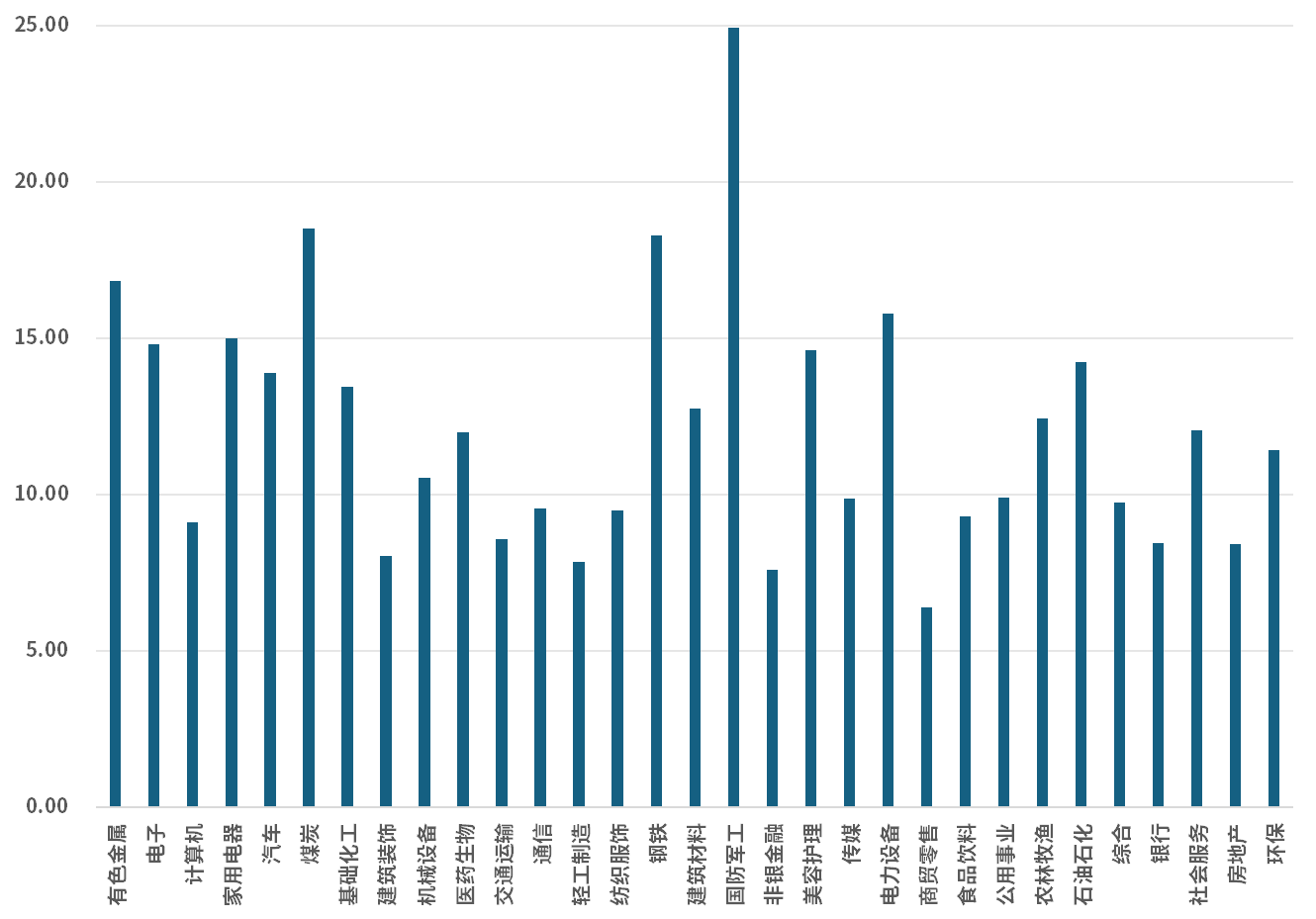
数据来源:衡泰一数通、财汇、衡泰研究部
由上可知,相对于风格因子,行业因子的风险和显著性占比更高,行业因子中最低的年化波动率(6.4%)依旧仅仅低于风险最高的风格因子(7.59%)。
回归显著性占比靠前的5个风格因子分别为Momentum, Beta, Size, Resid_vol, 和Non-line,其中Beta和Size因子的年化波动率分别达到7.59%和5.37%,回归显著性占比高达64%和52%,因此投资中如果想降低组合波动率,控制行业、市值和Beta的风险相当有效。
3.4 市场因子收益率统计
对于多因子模型,因为全市场的流通市值加权的风格因子暴露之和为0,以及流通市值加权的残差收益率之和几乎为0,所以全市场的流通市值加权收益率之和(即全市场组合收益率)几乎等于市场因子收益率。
全市场组合收益率是否等于市场因子收益率,这是验证多因子模型的一个极其重要的标准。我们以恒生综合指数收益率代表全市场组合收益率,计算市场因子月收益率和恒生综合指数月收益率的差值。如图所示,差值围绕0上下波动,均值为0.1%,最大差异不超过3.5%,说明模型良好。
图6:市场因子收益率与恒生综合指数收益差值(%)
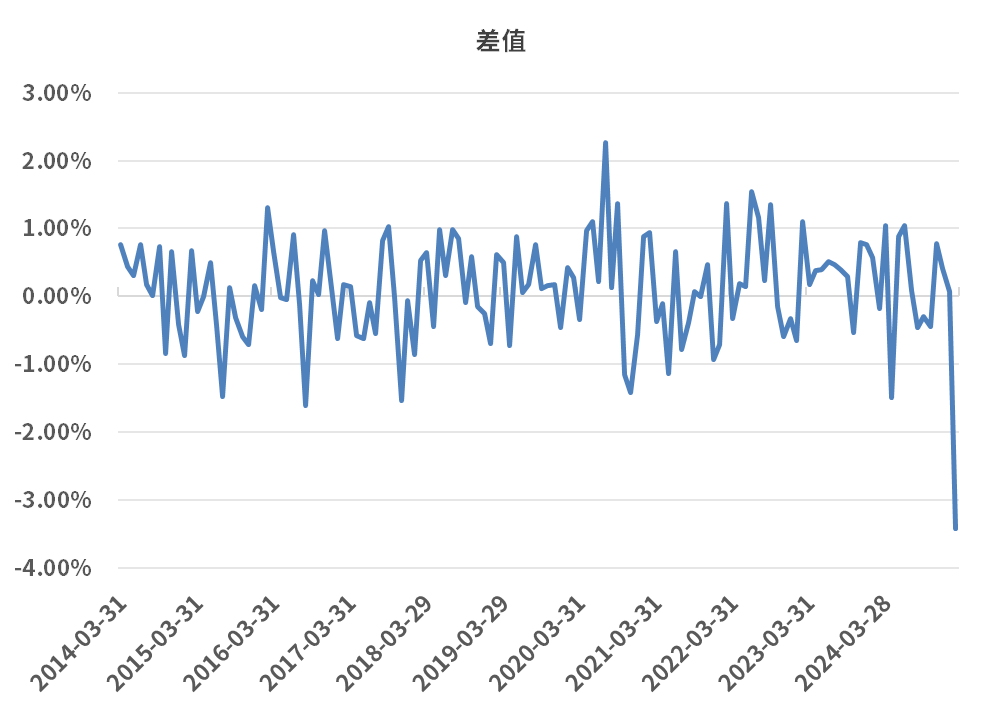
数据来源:衡泰一数通、财汇、衡泰研究部
为更精确的展示两者关联,我们构建地区(市场)因子收益率累计净值曲线,与恒生综合指数累计净值曲线进行对比。可以发现两者的走势几乎完全一致,细微差别是因为指数构建规则而导致(指数收益率是自由流通市值加权且使用分级靠档,不考虑现金分红;地区因子收益率和全市场组合收益率相当于是流通市值加权)。地区因子的CAGR(年化复合收益率)为4.03%,恒生综合指数的CAGR为2.80%,两者的差异1.23%主要是由于股票现金分红而造成的。
图7:xHK1地区(市场)因子累计净值和恒生综合指数累计净值对比
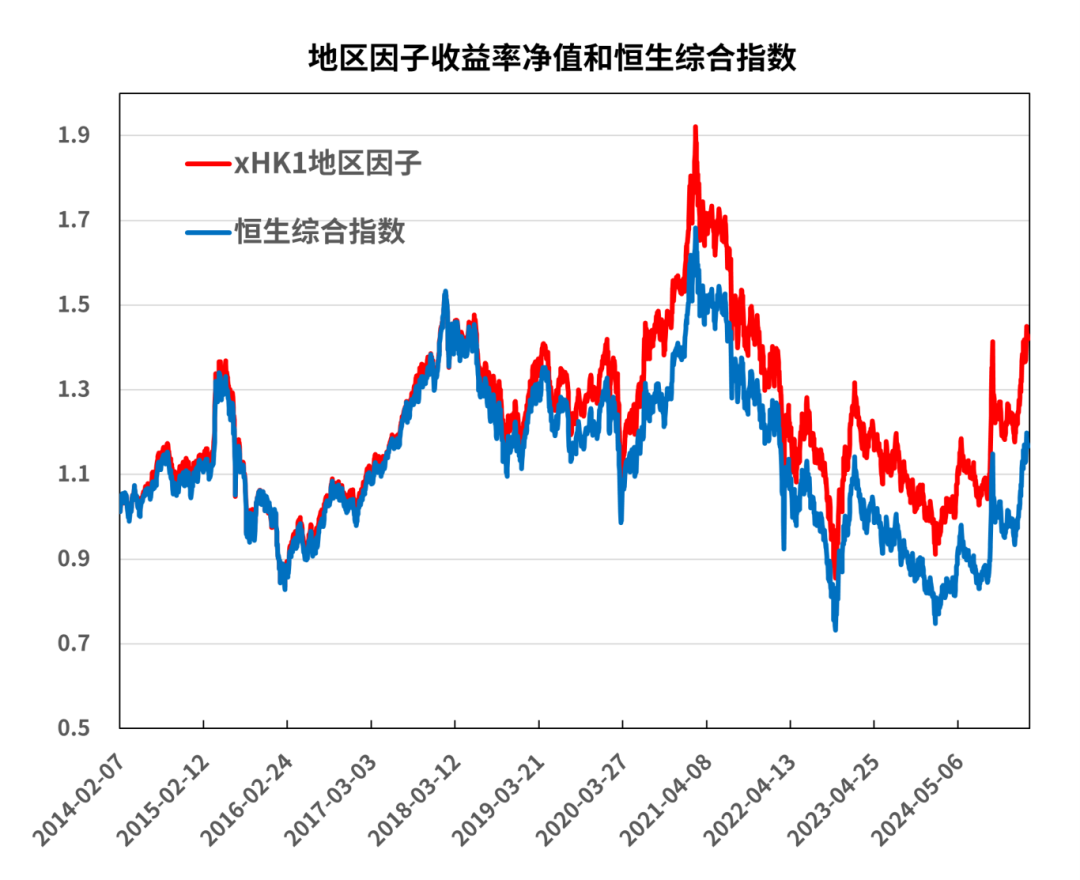
数据来源:衡泰一数通、财汇、衡泰研究部
3.5 风格因子收益率统计
通过统计各期的横截面回归T值,可以检测因子对股价收益率的影响显著性。一般|T|>2代表有显著影响,|T|>2的周期占总周期的比例代表因子是否有稳定的显著影响。
xHK1模型的风格因子在因子解释力显著性和稳健度均有较好表现。具体来看:
1) 从显著度角度:各风格因子的|T|均值为1.83,其中6个因子的|T|大于2,说明这些因子对港股市场具有较高的解释度。
2) 从稳健度角度:各风格因子“|T|大于2占比”的均值为34%。
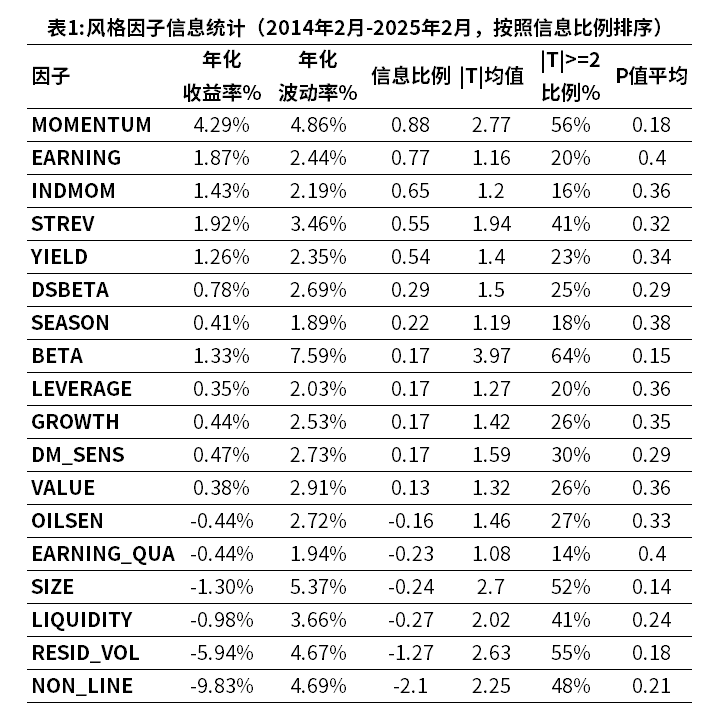
数据来源:衡泰一数通、财汇、衡泰研究部
如表1所示,港股市场风格总体呈现如下特征:
- MOMENTUM(1年的个股收益率),INDMOM(所属3级行业的6个月收益率)呈现动量效应
- STREV(3个月的个股收益率乘以-1)呈现反转效应
- EARNING,YIELD 呈现低估值效应
- 呈现低波动率(resid_vol)效应,低换手率(liquidity),低non-line效应
- 呈现小市值(size)效应
我们发现A股模型的10个因子收益率均值的正负号和港股模型完全一样,反映港股市场的整体风格特征和A股市场接近。港股和A股的3个月收益率都呈现反转效应。
相比之下,美股在同样的时间维度更多是呈现动量效应,在5天的时间维度则呈现反转效应。低估值效应和小市值效应在A股,港股,和美股市场里都长期存在,反映投资者确实把低估值做为选股的考量标准之一,以及小盘股长期而言具有超额收益。
图8和图9展示2024年表现最好和最差的五个风格因子。2024年全年表现最好的风格因子是短期反转因子STREV。2024年9月,央行联合多部门推出降准(释放约1万亿元流动性)、降息(逆回购利率下调)、降低存量房贷利率(平均降幅0.5%)和二套房首付比例(至15%)等政策组合拳,缓解市场资金压力并提振房地产行业信心,这期间表现最好的是β因子,高β股票远远跑赢其它股票。2024年全年表现最差的风格因子是非线性因子Non-line,说明24年应该超配Non-line因子暴露度小的股票。
图8:表现最佳五个风格因子累计净值
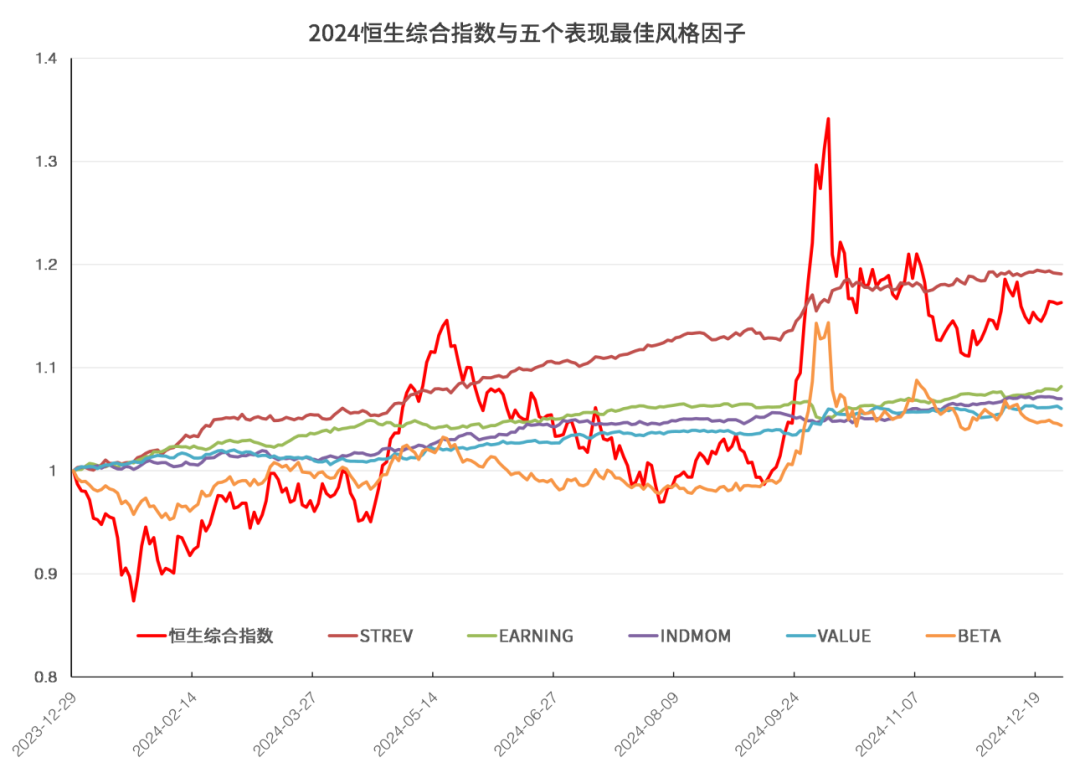
数据来源:衡泰一数通、财汇、衡泰研究部
图9:表现最差五个风格因子累计净值
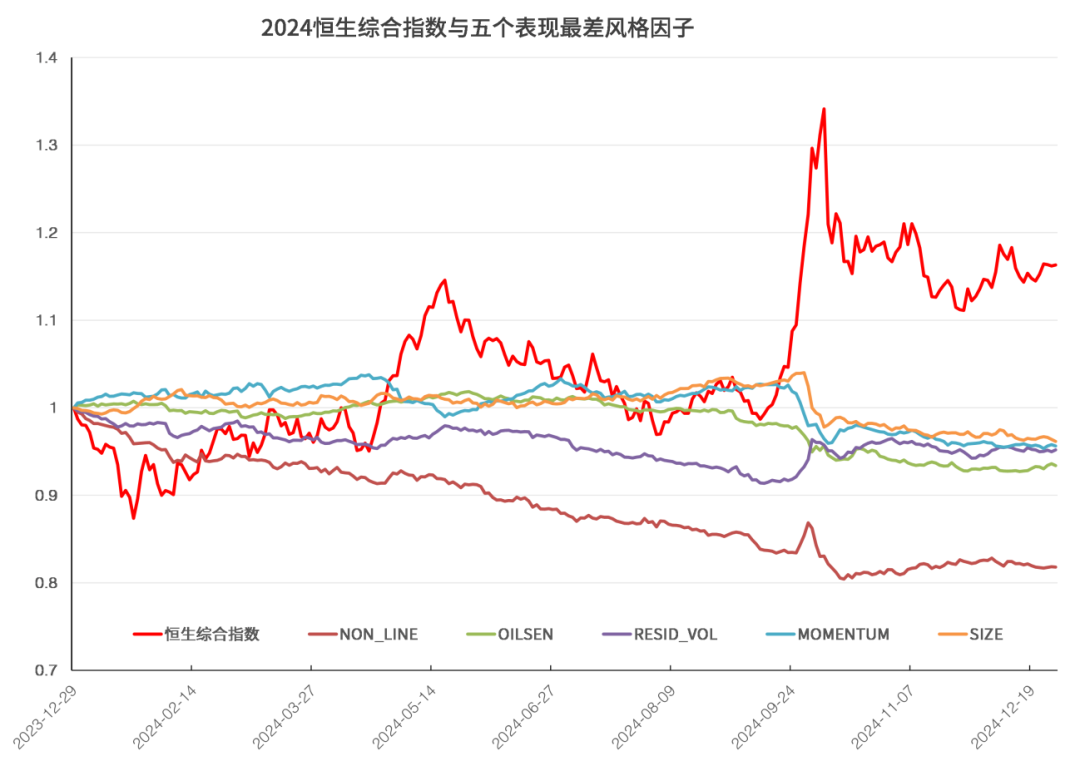
数据来源:衡泰一数通、财汇、衡泰研究部
3.6 行业因子收益率统计
注意到行业因子收益率是剔除了国家因子收益率的,本来其实应该叫行业因子超额收益率。但约定俗成,我们还是叫它行业因子收益率。在31个申万行业中,信息比例排名靠前的5个行业分别是有色金属、电子、计算机、家用电器、和汽车。
从收益率来看,有色金属和电子行业近10年有显著超额收益。相对于风格因子,行业因子整体年化波动率较高,大约是风格因子年化波动率的4倍左右,因此控制行业风险在选股配置中不容忽视。
xHK1模型的行业因子在因子解释力显著性和稳健度均有较好表现。具体来看:
1)从显著性维度:各风格因子的|T|均值为2.78,其中24个因子的|T|大于2。
2)从稳健度维度:各风格因子“|T|大于2占比”的均值为50%。
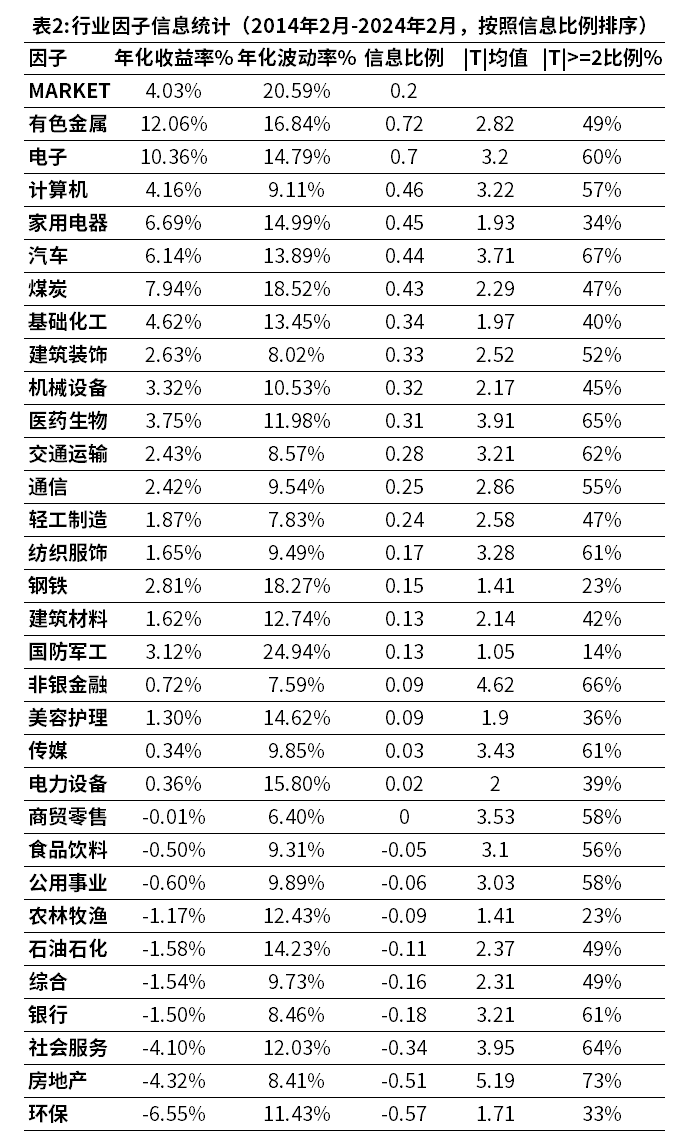
数据来源:衡泰一数通、财汇、衡泰研究部
图10和图11展示2024年表现最好和最差的五个行业因子。2024年全年表现最好的行业是电子。在2024年9月的政策组合拳期间,表现最好的是非银金融,其次是电子。2024年全年表现最差的行业是农林牧渔。
图10.表现最佳五个行业因子累计净值
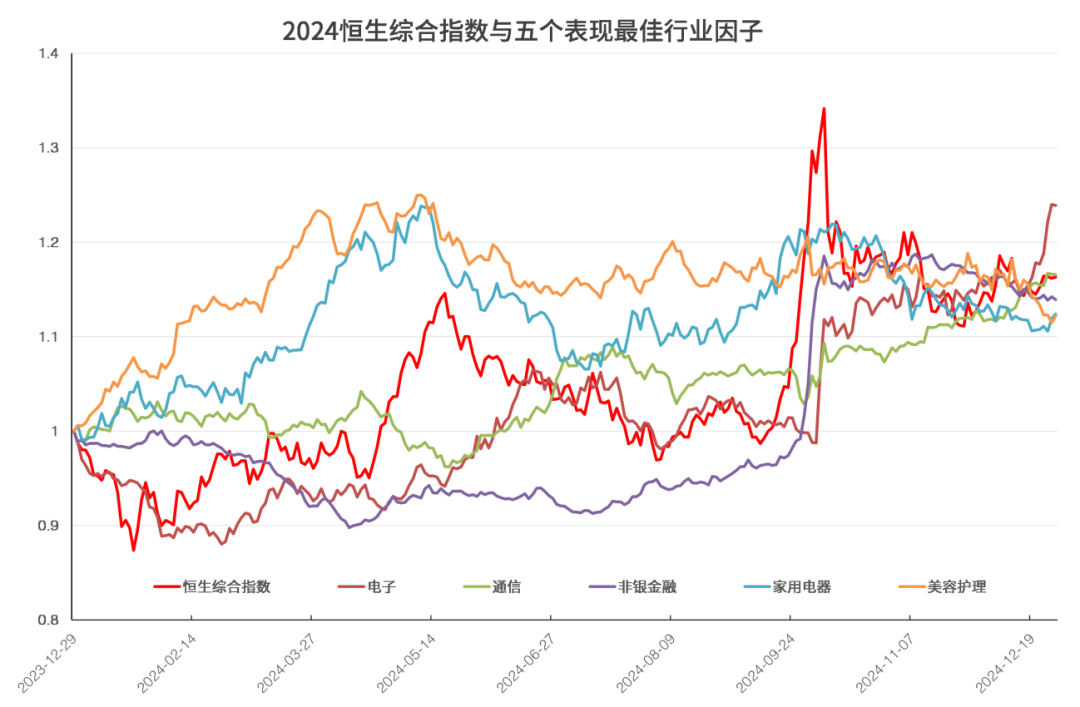
数据来源:衡泰一数通、财汇、衡泰研究部
图11.表现最差五个行业因子累计净值
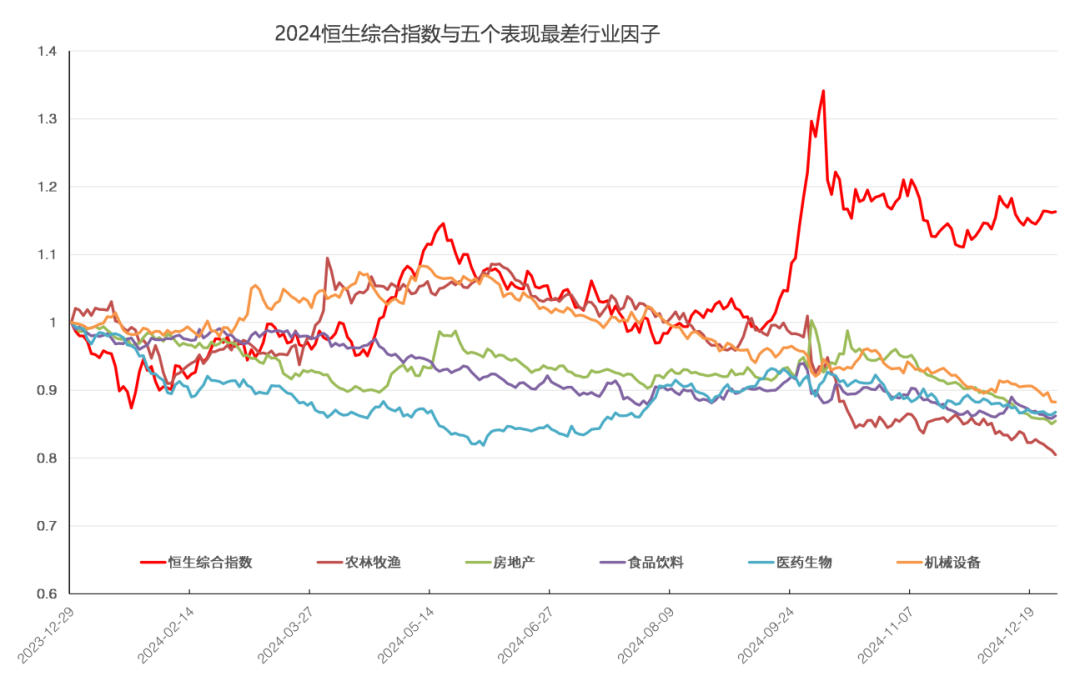
数据来源:衡泰一数通、财汇、衡泰研究部
04
结论
风险模型对投资组合分析主要有如下的作用:降低投资组合的风险暴露,实现更精确的风险管理,提供更准确的组合优化结果,进行更有效的绩效归因和风险归因。本文主要对衡泰多因子模型方法理论和模型实证结果做了详细介绍。
我们参考Barra的CXE1模型,使用18个风格因子,同时将行业替换为符合中国本土市场的申万行业分类,构建衡泰港股多因子模型xHK1,并在港股市场进行实证。实证结果主要从以下3个方面阐述:因子对港股收益率的整体解释度,因子收益率的波动率,因子解释力的显著性和稳健度。
从2014-2025年,xHK1模型的平均拟合度Total-R2达到20%。风格因子的平均因子收益率波动率为3.37%,|T|值的均值为 1.83,“|T|值大于2占比”的均值为34%;行业因子的平均因子收益率波动率远高于风格因子,为12.05%,|t|值的均值为 2.78,“|T|值大于2占比”的均值为50%。总体而言,衡泰xHK1模型对港股收益率具有良好的、符合预期的解释能力。
搭载A+H股多因子模型的
衡泰多因子系统
现已正式推出!
系统路演开放申请中
xAsset-FM 衡泰Asset多因子系统,现面向金融机构开放路演申请,详情可联系对接销售。
权威研究与实证
衡泰多因子团队,在金融投研、定量分析及技术领域拥有深厚积淀,深入研究全球多因子理论与实证,成功实现了多因子模型中国市场的本土化创新应用。多篇团队实证研究成果,可点击查看:
《衡泰多因子风险模型介绍及A股实证》
《Brison、多因子归因模型对比及创新应用》
《组合风险预测:多因子模型协方差矩阵调整》
《多因子模型的协方差矩阵调整》
《2023年A股市场因子分析》
此外,《投资管理》/China JOIM“多因子与基金评价”专刊,从定量分析角度,汇集全球权威研究与实证,并通过中国数据验证研究方法对中国市场的适用性。详情或订阅请点击。
衡泰多因子团队,由衡泰首席量化专家、拥有25年以上国际与国内投资机构投研经验的吴卫东博士领衔,汇聚资深金融定量分析师与金融科技工程师,实现定量研究与IT技术的深度融合,打造出可比肩国际顶尖厂商的多因子模型与系统。
